|
BEL
CHEN
&
Co
|
|
The Game
of Life
|
Here is run-down of the theme considered on a forum http://lib.mexmat.ru/forum/viewtopic.php?t=2376 in Russian.
Boris Lejkin has offered the following alternative of Life with several alive states: Rule S23/B3 is fulfilled for cells of each ON state irrespective of others. If the dead cell has 3 neighbours in state A and 3 neighbours in state B birthes of a new cell do not happen.
As a program-viewer it utilised MCell with the user dynamic library, which source codes on C or on Delphi are here. Here is applied DLL for a case with 4 alive states.
Some interesting patterns:
Alternatives of a two-color pulsar.

Intersections of two beacons and two tripoles.

Oscillators with rotors of a beacon.

Oscillator with a bipole rotor. Deriving other analogs of a barberpole needs a bandage of other color.
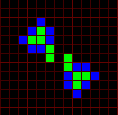
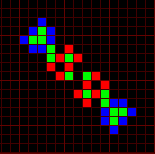
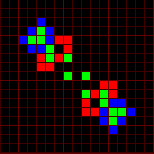
Variants of a p15 oscillator.
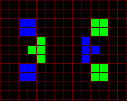
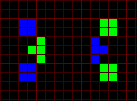
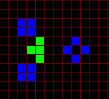
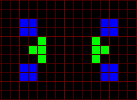
Replacement of blocks by the sparkers I found has allowed to build new p15 oscillator working in routine Life.
p24 and p30 oscillators.
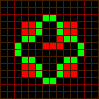
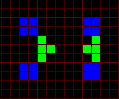
4c/15 and Pi conduits.
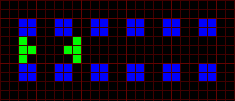
![]()
p104 gun.

The analysis has shown, that a determination of new patterns in Lejkin's model is a simplis problem, than in Life. Symmetric inductors have on 2 alternatives distinguished by a breadth on 1 cell. If one of states presented only by still-lifes they cannot be destroyed by any processes happening to other states. It allows to stabilise simplese some rotors for which in Conway's Life stabilization is impossible or complicated sparkers or eaters would be necessary. Detection new p15 oscillator shows, that it is possible to use Lejkin's rules as the auxiliary tool by searching new patterns in Life.
2006 may 16
Nicolay Beluchenko