Мир, который построил Конуэй

Добро пожаловать в плоскую клеточную вселенную — вселенную, в которой живут удивительные организмы Конуэя. Свойства этой вселенной уже более 30 лет изучают математики и просто увлеченные игрой «Жизнь» (Game of Life) энтузиасты.

С точки зрения математики мир игры Life не является плоскостью — это дискретное множество, элементы которого связаны соотношением «близости». Такие множества обычно называют графами. Элементы множества в «Жизни» имеют ровно по 8 соседей и легко представляются в виде бесконечной плоскости, расчерченной на клетки. Все клетки, имеющие хотя бы по одной общей точке с данной клеткой, считаются соседними с ней.

Возможны другие дискретные множества, в которых элементы имеют другое число соседей, или число соседей различно для разных элементов, или даже число соседей равно 8, но эти 8 элементов по-другому связаны между собой. Для них тоже можно построить нечто подобное нашей игре «Жизнь», но это будет уже другая игра, и в ней все будет по-другому.

Что же превращает дискретное клеточное множество в Life? Во-первых, элементы этого множества могут находиться в двух состояниях (в Игре эти состояния называются «организм» и «пустая клетка»). Во-вторых, в игре Life вводится (тоже дискретное!) время. Состояния элементов (клеток) меняются во времени в зависимости от числа соседних «организмов». Так, если «сейчас» организм имеет 2 или 3 соседних организма, он в следующий момент времени (или, как говорят, в следующем поколении) останется организмом, т.е. выживет. Если же из 8 соседних элементов число организмов составит менее 2 или более 3, то организм изменит свое состояние, т.е. в следующий момент времени станет пустой клеткой (умрет). При этом, по аналогии с настоящими живыми существами, он умрет либо от одиночества (число соседей 0 или 1), либо от тесноты (число соседей более 3). Пустая же клетка может стать организмом (говорят, что «родится» новый организм), только если около нее присутствует ровно 3 организма. Эти правила или «законы эволюции» придумал создатель «Жизни» Конуэй.

Другие математики следом за Конуэем исследовали аналогичные дискретные пространства с другими законами эволюции, среди них были также достаточно интересные «миры», но только Game of Life приобрела такую огромную популярность: десятки тысяч исследователей искали и находили сотни тысяч красивых конфигураций, сотни компьютерных программ были созданы для решения задач, возникающих при рассмотрении этой игры.

Итак, повторим для себя, что же такое «Жизнь»? Это бесконечное плоское клеточное поле, состоящее из пустых клеток и организмов. Развитие любой конфигурации определяют 2 закона:

1. организм выживает, если имеет 2 или 3 соседей и умирает в противоположном случае;
2. новый организм рождается, если число соседей равно 3.

Оказывается, при таких простых правилах мир «Жизни» удивительно разнообразен. Если одиночный организм, окруженный только пустыми клетками, в следующий момент времени умирает (то же самое можно сказать и о паре организмов), то уже при трех организмах на поле мы можем получить объект, называемый мигалкой.

Из трех организмов, расположенных в ряд, в следующий момент умрут только два крайних, зато 2 новых организма родится по обе стороны от среднего организма. Таким образом, горизонтальный ряд из 3 организмов в следующем поколении превращается в вертикальный ряд из 3 организмов и наоборот. В целом мигалка, периодически изменяясь, становится «вечно живой».

Именно свойство образовывать более сложные и более устойчивые объекты, живущие на клеточном множестве, и обусловило интерес к Life. Это свойство напоминает образование многоклеточных организмов в живой природе. Что мы представляем из себя, как не колонию живых и достаточно простых клеток, поддерживающих жизнь друг друга и всего организма за счет отмирания одних клеток и рождения других?

Уже из 4 организмов можно собрать стационарный, т.е. вечно живущий и не изменяющийся во времени ансамбль: блок.

При большем числе организмов появляется огромное количество стационарных конфигураций (или, как говорят, "натюрмортов"): бадья, лодка, корабль, змея, длинная змея...

...улей, каравай, пруд, длинная лодка, длинный корабль…

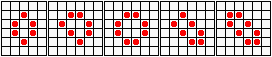
...баржа, рыболовный крючок, шляпа, авианосец...

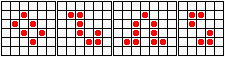
...соты, тонущий корабль, дубинка, длинная баржа и т.д.

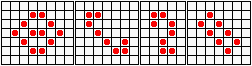
Не менее разнообразны и периодические колонии ("осцилляторы"): бакен, часы, жаба…

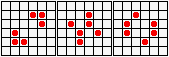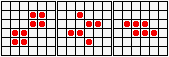
...восьмерка, пентадекатлон, тумблер...

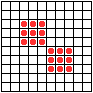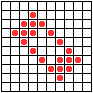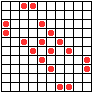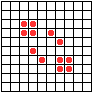
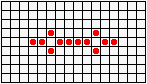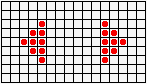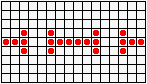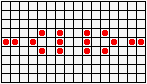
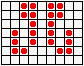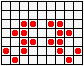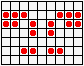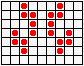
...пульсар, бриллиантовое кольцо, вертушка и т.д.

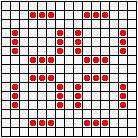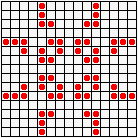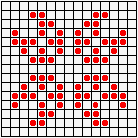
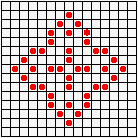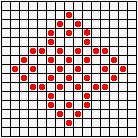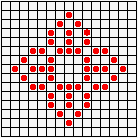
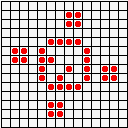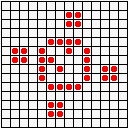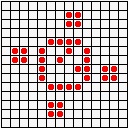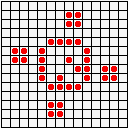
Но особенно интересен глайдер,
состоящий из 5 «элементарных» организмов. Эта конфигурация не только периодически меняет свою форму, но и смещается на плоскости, двигаясь по диагонали. Есть в игре Life объекты, способные передвигаться и в горизонтальном направлении. Это так называемые космические корабли.

И здесь самое время поговорить о терминологии. Когда мы называли стационарные и периодические конфигурации вечно живущими, бессмертными, имелось в виду их неограниченное во времени существование в неизменном или периодически изменяющемся виде. Но для истинной жизни характерна эволюция, а не вечное повторение, поэтому такое бессмертие ближе к неизменности мертвых предметов и процессов неживой природы, чем к вечно изменяющемуся потоку живой материи. К тому же, наблюдая развитие многих конфигураций, мы видим, как бурный хаотический с виду процесс постепенно приводит к набору из натюрмортов и осцилляторов, после чего ситуация становится полностью предсказуемой, т.е. не интересной. Поэтому логично называть периодические конфигурации мертвыми, а время перехода от исходной конфигурации до осциллирующей — временем жизни конфигурации.

Большинство колоний (если их набирать случайно — что позволяют делать некоторые компьютерные реализации Life) относительно недолговечны. После нескольких десятков, от силы сотен поколений жизнь на клеточном поле прекращается, оставив после себя набор мигалок, блоков, ульев и прочих «останков», да еще какое-то количество глайдеров стремительно удаляется прочь от погибшей клеточной цивилизации в тщетной надежде наткнуться на что-то в пустом клеточном космосе. Поэтому всегда интересны колонии, способные жить долго, особенно если их исходное состояние достаточно малочисленно. Из таких долгожителей наиболее известны r-пентамино — 1103 поколения и желудь — 5206 поколений (на рис. показаны начальные конфигурации).

Движущиеся объекты, например, глайдеры, можно с полным правом считать переносчиками жизни. Часто можно наблюдать, как вылетевший из одной части колонии глайдер движется к другой ее части, в которой всякие признаки жизни уже исчезли (т.е. остались только мертвые объекты), а после столкновения в этой уже умершей части вновь вспыхивает бурный процесс. Например, в конфигурации, изображенной на рисунке, глайдер попадает в голову мертвой змеи, тело которой тут же начинает бурно разлагаться, пока не превращается в небольшой набор более простых неживых объектов, а в процессе разложения система испускает два глайдера, не считая исходного, который не погибает в столкновении, а просто отражается от твердого змеиного лба.

Некоторые стационарные или периодические объекты способны поглощать глайдеры, приближающиеся к ним под определенным углом и в определенной фазе (не забудем, что глайдер периодический объект), например, блок, пентадекатлон. Особенно устойчив рыболовный крючок, способный поглотить самые различные формы жизни.

Другие объекты являются вечными источниками глайдеров. Это так называемые глайдерные ружья.

Комбинации глайдерных ружей, расположенные специальным образом так, чтобы выпускаемые ими глайдеры, сталкиваясь, порождали новые объекты, иногда дают весьма интересные картины.