
Прежде всего одно вводное замечание. Практически все примеры в этой статье приведены в виде анимированных GIF-изображений, так что вам не понадобится для их просмотра каких-либо специальных программ. Если же вы хотите сохранить какие-то примеры с тем, чтобы позже можно было бы их просмотреть программой Жизни (например, Life32), то вы можете скачать соответствующие файлы, кликнув на нужном рисунке (или, если рисунка нет, на ссылке).
Блок — это простейшая устойчивая конфигурация из 4 клеток, которая является своеобразным символом устойчивости в Жизни. Если он и принимает участие в реакциях, то преимущественно в качестве катализатора, изменяясь только на время взаимодействия и восстанавливая к концу реакции свой первоначальный вид и положение. Поэтому говорить о движении блока — это посягать на святая святых. Мы и не будем этого делать, считая, что то, что будет показано далее — это только визуальный эффект движущегося блока. Тем более, что практически во всех наших примерах блок не будет изолированным от других ячеек (т.е. не будет занимать отдельного кластера), а будет находиться в постоянном взаимодействии с ними.
Именно это взаимодействие может поглотить две ячейки блока, а с другой стороны породить две новые, создав иллюзию перемещения блока. Вот пример из коллекции lifep.zip (это одно из самых популярных собраний образцов Жизни), в котором блок последовательно перемещается в одну и в другую сторону, совершая, таким образом колебания с периодом 2.

Если придерживаться строгости, то в данном осцилляторе только 4 ячейки изменяют свое состояние — их обычно называют ротором осциллятора. Все остальные ячейки неподвижны и составляют статор. В статор входят и 2 центральные ячейки блока. Но мы в этой статье не будем слишком строги и будем считать, что блок (состоящий, естественно, из 4 ячеек) движется, а то, что его окружает — это только опора для него (в следующих примерах и эта опора будет меняться, т.е. содержать ячейки ротора, но эти изменения мы будем считать не слишком важными, выделяя то, что бросается в глаза). Конечно такой подход не самый правильный, но нас в этой статье интересует именно визульный эффект.
Другой пример из этой же коллекции содержит уже 2 блока, снующие в противоположных фазах. Причем если размер первого образца (точнее, размер ограничивающего его прямоугольника) был 12×9, то этот образец даже меньше (9×9). То есть два колеблющихся блока за счет взаимодействия друг с другом более компактны, чем один.

А это уже найденный мной (* см. дополнение 1) осциллятор, содержащий три блока-челнока. Он только чуть больше предыдущего образца и все еще меньше самого первого. Обратите внимание, что опора в этом образце также колеблется с периодом 2.

Количество последовательно противофазных снующих блоков может быть любым и образовывать нечто похожее на коленчатый вал. При этом количество возможных типов опор (если уж мы назвали блоки коленчатым валом, то опора для него — это подшипники) для образца ширины 9 ограничено числами 4 (промежуточные подшипники) и 2 (оконечные подшипники). Все эти типы можно увидеть на диаграмме.

Таким образом мы можем построить коленвал бесконечной длины. Бесконечные осцилляторы в Жизни принято называть фитилями. Естественно, я не могу изобразить бесконечную конфигурацию и вынужден применить оконечные подшипники (в общем случае это называется окончания или заграждения), чтобы обрезать фитиль. Так обычно и поступают при демонстрации фитилей, считая, что человек, рассматривающий обрезанный фитиль может уловить закономерность его структуры и мысленно продлить его до бесконечности.
А это коленвал несколько иной кострукции.

Можно также построить фитили с блоками-челноками, расположенными вдоль направления движения. Это три из них, причем первый взят из коллекции lifep, а два других найдены мной. Обратите внимание, что в первом образце блоки совершают более крупные скачки, сдвигаясь в каждом поколении сразу на две клетки.
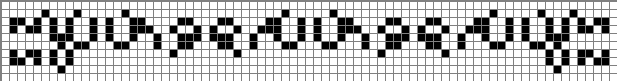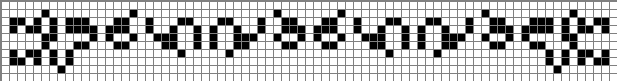

Однако, поскольку блоки в этих фитилях не взаимодействуют непосредственно друг с другом, то они менее интересны, чем их поперечные собратья.
Осциллятор, показанный ниже, интересен тем, что в него входят окончания другой очень любопытной конфигурации, которая называется полюсником или палкой. Английское название ее barberpole, что буквально означает "шест цирюльника". Дело в том, что в Европе парикмахеры всегда устанавливали около своих заведений полосатый шест, как знак парикмахерской, а полюсник очень напоминает полосатую палку. Мы называем его полюсником, так как pole означает не только шест, но и полюс, и еще потому, что полюсники различной длины принято называть bipole, tripole, quadpole и т.д., что соответствует нашим биполь, триполь, квадруполь и т.д. Полюсник тоже может быть продлен до бесконечности, т.е. тоже является фитилем.

К нашему осциллятору можно пристыковать куски полюсника любой длины, превращая участок со снующим блоком в подобие кусочка мяса, насаженного на шампур (при этом шампур сдвигается на кусочке мяса в сторону на одну клетку). Более того, на полюсник можно насадить любое количество кусочков мяса.
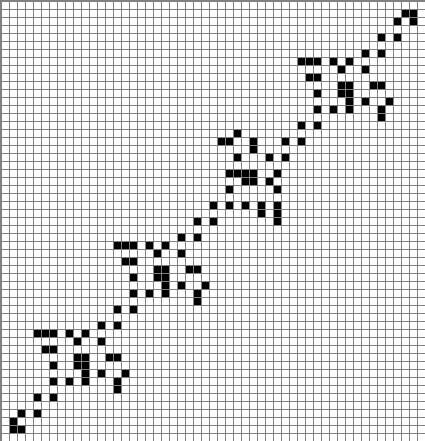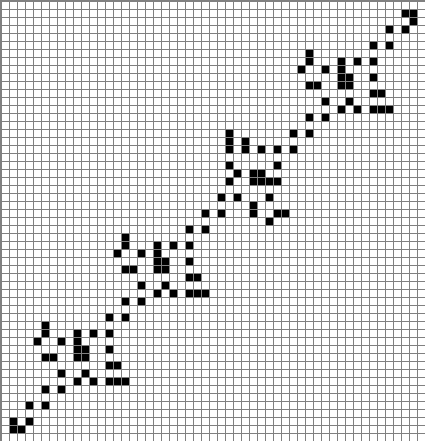
Если кусочки мяса придвинуть вплотную друг к другу, так, чтобы участки полюсника между ними практически исчезли, можно получить следующие фитили.


Следующие два образца интересны только своей формой — это скакалка и велосипедист.
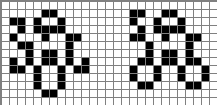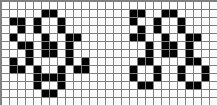
Все предыдущие примеры имели период 2. Но эффект снующего блока возможен и в других периодах. Вот осциллятор периода 4, в котором блок движется в 2 раза медленнее, чем в случае периода 2.

А в этом p4 осцилляторе увеличена амплитуда возвратно-поступательных движений блока за счет того, что он делает по два шага в каждую сторону.

Образец периода 3 дает пример подпрыгивающего блока: на протяжении двух поколений блок неподвижен и только в третьем поколении сдвигается на одну клетку, чтобы сразу же вернуться обратно.

Вот еще один образец из коллекции lifep, в котором блок совершает диагональные колебания.

Этот образец во многом похож на "кусочек мяса", т.е. к нему с двух сторон можно присоединить полюсник. Эти образцы, соединяясь между собой, также могут образовывать фитили.


А это еще один осциллятор, в котором блок совершает диагональные движения. Здесь движения блока очень эффектно дополняются движениями двух плюсов (их правильное название — X-пентамино).

Близким к рассматриваемой теме можно считать известный фитиль периода 5, который называется "муравьи". Он отличается тем, что блоки в муравьях во всех поколениях имеют прикрепленные с боков "ноги". Кроме того, муравьи не совершают возвратно-поступательных движений, а движутся все время в одном направлении. Желающие могут посмотреть этот фитиль, например, в Словаре Жизни или скачать файл ants.lif.
А вот пример, в котором блок (опять же это не совсем блок — вместе с точкой, "приклеившейся" к нему, он называется P-пентамино) вращается с периодом 4 вокруг одного из своих углов. Вокруг него движется по орбите еще один блок (который тоже не совсем блок). Все это вращение поддерживается четырьмя жабами (эти жабы тоже только похожи на жаб — на самом деле они имеют период 4 вместо периода 2, полагающегося настоящей жабе). К каждой из жаб с противоположной стороны можно приставить еще одну вращающуюся конструкцию и продлить образец во все стороны до бесконечности — такие образцы называются агарами. Пример агара жабий ротатор (тоже обрезанный с помощью специальных окончаний) имеет довольно большие размеры, поэтому мы не стали показывать его изображение здесь, а приводим только одну его элементарную ячейку.

Немного похожий, хотя и достаточно тривиальный пример циклического перемещения блока можно получить, если воздействовать на него потоками глайдеров. В файле p46bh.lif мы построили такой пример, использовав 4 глайдерных ружья периода 46.
Я выражаю благодарность создателям программы WinLifeSearch Дэвиду Беллу, Джейсону Саммерсу и Карелу Сухайде. Без этой программы данная работа была бы невозможна.
| Николай Белюченко |
Дополнение.
1. Уже после размещения этой статьи в интернете я обнаружил в "коллекции марок" Дина Хикерсона пример, содержащий 3 снующих блока, показанный выше. Он был найден Дином Хикерсоном еще в 1993 году. В этом нет ничего удивительного: трудно расчитывать на новизну результата, производя поиск в такой исследованной области, как осцилляторы низких периодов.
2. Я также провел поиск осцилляторов, в которых колеблется не блок, а плюс (X-пентамино). Желающие могут увидеть некоторые результаты в файле shplus.lif.