| Теория симпатий> | Письмо 1 — введение в теорию Письмо 1 — симпатии интересов Письмо 1 — классификация Письмо 2 — согласия Письмо 2 — размерность | Архив статьи |

| Теория симпатий> | Письмо 1 — введение в теорию Письмо 1 — симпатии интересов Письмо 1 — классификация Письмо 2 — согласия Письмо 2 — размерность | Архив статьи |

Женя, ты, конечно, понимаешь, что все это пишется не в один присест. Кое-что я вспоминаю, другое продумываю заново, совершенно переделывая. Некоторые определения изначально не точны и их приходится повторять. Кроме того, чтобы ни ты не устал читать, ни я не устал писать, я считаю допустимыми может не всегда точные, но достаточно яркие, на мой взгляд, аналогии и даже лирические отступления. Простых доказательств я не привожу, т.к. считаю, что если тебе это интересно, то ты и сам сможешь доказать достаточно очевидные вещи, а если это все писать, то уж, скорее всего, будет просто неинтересно. Формул тоже очень мало, т.к., во-первых, это все-таки теория множеств, где их вообще немного, а во-вторых, мне интереснее донести суть словами, аналогиями, примерами.
Возможно, к некоторым разделам придется вернуться и, скорее всего, придется ввести оглавление, т.к. уже сейчас без плана ориентироваться в написанном становится трудно. Но, вернемся к теории. Прежде, чем перейти к новой теме, скажу еще пару слов о раскольцевании. Раскольцевание, как и любое сокращение, заменяет некоторые подмножества исходной симпатии (для раскольцевания — циклические подмножества) на отдельные элементы. Чисто теоретически такая процедура приводит к появлению симпатии более простой по структуре, чем исходная. Но в практических приложениях мы видим, что сокращение (и раскольцевание в частности) приводит к появлению в симпатии элементов разных типов, т.е. симпатия становится неоднородной. Тем не менее все свойства ее как симпатии вполне однородны — новые «объединенные» элементы, как и старые «одиночные», обладают набором интересов, так же входят в наборы интересов других элементов. Это позволяет обращаться с существенно неоднородными системами, включающими как отдельные элементы, так и их различные объединения различных уровней, как с однородными. Необходимо только правильно определить интересы всех элементов, т.е. связи между ними. Все сказанное относится не только к раскольцеванию, но и к любому сокращению симпатии. Насчет раскольцевания же следует отметить следующее. Логическое основание для этой операции — избавиться от периодического появления элементов, входящих в кольцевые маршруты, в цепи поколений, т.е. сделать цепь поколений более удобной для рассмотрения путем «вычищения» из нее засоряющих элементов. После раскольцевания никакой периодичности в поколениях не наблюдается. Новые элементы, заменяющие кольцевые маршруты, находятся в своем времени. Но это вовсе не значит, что после раскольцевания «всяк сверчок знает свой шесток», т.е. каждый элемент появляется только в одном поколении. Рассмотрим, например, такой фрагмент симпатии:

Здесь, рассматривая будущее элемента 1, мы видим, что в 1-м поколении присутствуют элементы 2 и 3, во 2-м — 5 и 4, в 3-м — 6, 7 и 5, в 4-м — потомки элементов 6, 7 и сами элементы 6, 7. От такого размножения элементов в поколениях, связанного с существованием маршрутов разной длины между элементами, раскольцевание не избавляет.
А сейчас попробуем рассмотреть более практическую задачу, связанную с симпатиями. Как запрограммировать симпатию для компьютера, т.е. как объяснить тупой машине, с чем она имеет дело, чтобы в дальнейшем компьютер мог понимать, что от него требуется, когда мы попросим его, например, распечатать 5-е поколение элемента a282 или еще что-нибудь, что придет нам в голову. Надеюсь, рассмотрение такой «прикладной» задачки поможет и нам лучше понять, что же такое симпатия, и что такое — ее элемент.
Мы уже отмечали, что каждый элемент симпатии — это не просто элемент множества, а нечто более сложное — это элемент плюс некоторое подмножество, связанное с ним:
S = {ai, {aj}i}, где ai ∈ M, aj ∈ M.
Мы отмечали неоднородность понятия элемента: сам элемент — это его суть, нечто твердое, весомое; а элементы, входящие в область интересов — это только ссылки на элементы, это связи базового элемента ai. Поэтому для описания элемента симпатии больше всего подходит такое понятие, как запись (или структура — в зависимости от языка программирования). Типы данных типа записи присутствуют, например, в таком языке программирования, как Паскаль. Запись позволяет описать как единую переменную целую структуру, состоящую из частей различных типов. В нашем случае сам элемент может быть задан его именем (т.е. переменной типа STRING (строка) в Паскале) или номером (переменная целого типа или INTEGER). Т.к. это элемент множества, то от всех других признаков мы абстрагируемся, хотя в конкретной компьютерной базе данных может присутствовать (хотя бы для справки) еще куча свойств элемента, характеризующихся переменными самых различных типов. Так, если этот элемент — дом, то там могут быть его площадь, кубатура, площадь приусадебного участка, наличие удобств, имя хозяина, адрес, год постройки, планировка комнат, фотография фасада и т.д. и т.п. Нас интересует вторая часть элемента — подмножество Mi, характеризующее интересы элемента. Описывать в этой части все базовые свойства элементов, относящихся к области интересов данного элемента — это дублировать многократно саму базу данных. Даже если указать здесь только основное свойство элемента (его имя или номер, или — для дома — почтовый адрес), то это приводит, с одной стороны, к ненужному дублированию (так, если имеем множество людей, то для каждого в область интересов надо вписать фамилии, имена и отчества всех, с кем связан данный субъект), с другой стороны, усложняет поиск элемента по ссылке. Ведь поиск нужной строки не такая уж простая процедура, и даже поиск нужного номера заставляет вновь и вновь просматривать базу данных.
К счастью, ничего подобного и не нужно. Можно в качестве ссылок на другие элементы вписать просто адреса этих элементов в памяти машины. Для этого служит переменная типа POINTER. Сослаться на адрес в памяти — это самое простое для логики программы — ничего искать не надо. Причем, для выяснения свойств системы, как симпатии, нам вообще не нужны ни имена переменных, ни их номера, ни другие данные. Нас интересуют только ссылки на другие элементы, т.е. только адреса в памяти. Поэтому мы можем отбросить «сам элемент» и считать, что элемент симпатии — это набор ссылок, набор адресов в памяти, где хранятся такие же списки других адресов. Таким образом, мы приходим к идеализированному машинному образу симпатии, как множеству списков адресов списков.
Конечно, в конкретной реализации нам понадобятся и базовые данные самих элементов, но они нужны только для справки, для идентификации элементов симпатии, как реальных объектов. Все же «системные» свойства элементов содержатся только в списках ссылок.
Таким образом, для симпатии собственное имя элемента (то, что мы обозначали ai) — это ничто, это только средство идентификации. Вся суть элемента в списке его ссылок. Симпатия — это множество списков ссылок, множество связанных между собой подмножеств. Представляешь? Множество, состоящее не из элементов, а только из подмножеств, каждое из которых — это тоже множество подмножеств исходного множества. А элементов, «как таковых», вообще нет.
Вот к каким выводам можно прийти из «практического» приложения. Поскольку именно к этим выводам я и вел, то более подробно о программировании симпатий писать не буду. Я думаю, запрограммировать работу с симпатией не слишком сложно, хотя и громоздко. И любой квалифицированный программист с этим справится. Признаюсь, я чуть-чуть слукавил, рассмотрев только случай, когда вся симпатия помещается в памяти. Более реален случай симпатии как базы данных, там все будет немного по-другому, но смысл моих выводов не изменится.
Попробуем еще разочек посмотреть «вглубь» симпатии. Поскольку симпатия, по сути дела, это система связей, то посмотрим, что получится, если в качестве элементов множества взять связи исходной симпатии. Т.е. мы рассматриваем множество ссылок данной симпатии, множество интересов всех ее элементов. Образуем на данном множестве симпатию по правилу: в качестве ссылок данного интереса мы берем множество интересов элемента, на который указывает данный интерес. Общее количество элементов в новой симпатии S1 (назовем ее симпатией интересов) равно сумме мощностей всех подмножеств интересов. Если мощность множества Mi обозначить [Mi], то количество элементов симпатии S1 равно
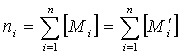 ,
,
где n — количество элементов симпатии S.
Попробуем подсчитать количество связей в симпатии интересов S1. Для элемента ai симпатии S мы имеем [Mi] связей. Но этот элемент упоминается в [M'i] областях интересов. Каждое упоминание элемента ai есть элемент симпатии S1, а для него каждый интерес образуется, как интерес элемента ai. Суммируя по всем элементам, имеем количество связей:
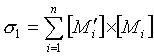 .
.
Естественно, σ = n1 количество связей исходной симпатии.
Для обозначения элементов симпатии интересов используется та же буква a, что и для элементов исходной симпатии S, но индексы будем ставить двойные — первый индекс соответствует номеру элемента симпатии S, от которого исходит интерес, а второй — номеру элемента, на который этот интерес направлен. Таким образом, если в симпатии S элемент ai имеет область интересов Mi, причем aj ∈ Mi, то в симпатии S1 будет присутствовать элемент aij. Область интересов этого элемента — это интересы симпатии S, относящиеся к области интересов элемента aj, т.е. множество Mj. Но множество Mj — это множество элементов симпатии S, а нам надо взять множество интересов, исходящих из элемента aj к элементам множества Mj. Обозначим их ajk, где индекс k пробегает все значения, удовлетворяющие условию ak ∈ Mj. Таким образом, симпатия S1 имеет структуру {aij, {ajk}ij}, где {ajk}ij = Mij — область интересов aij, причем эта структура однозначно связана со структурой симпатии S: aij существует, если aj ∈ Mi, а ajk входит в Mij, если ak ∈ Mj.
Т.к. выражение ak ∈ Mj не зависит от i, то от i не должно зависеть и его следствие ajk ∈ Mij, т.е. в определении области интересов Mij = {ajk}ij можно опустить индекс i: Mij = {ajk}j. Это ясно интуитивно из того, что область интересов элемента aij симпатии S1 строится как множество интересов элемента aj симпатии S и никак не связана с элементом ai той же симпатии. Таким образом, в симпатии S1 одну и ту же область интересов будут иметь элементы, имеющие одинаковый второй индекс.
Назовем элементы симпатии, имеющие одну и ту же область интересов, двойниками. Во многих случаях эти элементы ведут себя идентично — у них одно и то же будущее, все положительные поколения их совпадают, расстояния от них до других элементов симпатии также совпадают.
Таким образом, если в симпатии S существуют элементы, имеющие более одного интереса и не менее одного поклонника, то в симпатии интересов будут присутствовать двойники.
Что будет, если построить симпатию интересов от симпатии интересов данной симпатии? Так сказать, симпатию интересов второго порядка? Элементами этой симпатии будут интересы симпатии S1, т.е. связи ее элементов aij с элементами множеств Mij = {ajk}j. Обозначив их, по аналогии с элементами S1 через aijjk, мы видим, что в обозначении такого элемента всегда удвоен средний индекс, а соответствует он связи (ai с aj) со связью (aj с ak). Такой элемент существует, если в симпатии S существует элемент ai, причем в область интересов Mi входит элемент aj, в область интересов Mj которого входит элемент ak. Предыдущее предложение эквивалентно следующему высказыванию: элемент aijjk существует, если в симпатии S существует маршрут от элемента ai через элемент aj до элемента ak.
Возвращаясь назад к симпатии S1, мы видим, что ее элементы — это маршруты длины 1 симпатии S. Ведь интересы — это и есть маршруты длины 1. А элементы симпатии S2– это маршруты длины 2 симпатии S. Что касается интересов симпатий S, S1, S2, то они представляют собой маршруты длины 1, 2, 3 соответственно, начало которых совпадает с элементами этих симпатий (т.е. маршрутами длины 0, 1, 2). Таким образом, мы приходим к следующему выводу: симпатия интересов n-го порядка Sn на симпатии S представляет собой симпатию, элементами которой являются маршруты симпатии S длиной n, а интересами элементов — маршруты длиной n+1, начало которых на длине n совпадает с элементами.
По аналогии с этим введем более общее понятие: симпатия маршрутов. Симпатией маршрутов с длиной n и сдвигом k, где n≥0, k≥1, построенной на симпатии S, является симпатия Snk, элементами которой являются маршруты симпатии S длиной n, а в область интересов элемента m входят маршруты (длиной n) симпатии S, начало которых принадлежит к k–му поколению (в симпатии S) начала элемента m и, если k≤n, на длине n-k с начала совпадающие с концом элемента m.
Необходимо разъяснить один момент. Когда мы говорим об интересе или связи элемента, то мы говорим о маршруте длиной 1, а когда об области интересов, то по определению в нее входят элементы, а не маршруты (область интересов — это подмножество Mi множества M элементов). Поэтому в симпатии маршрутов мы говорим об области интересов, а туда входят сами элементы, т.е. маршруты длиной n. А в симпатии интересов n–го порядка мы рассуждали об интересах или связях между элементами, поэтому длина связи (как маршрута) была на 1 больше, чем длина элемента. Указывает же эта связь на элемент (маршрут длиной n), являющийся концом данной связи.
Исходя из определения симпатии маршрутов длиной n и сдвигом k, можно по-новому определить симпатию интересов n–го порядка. Симпатия интересов n–го порядка от симпатии S есть симпатия Sn1 маршрутов длиной n и сдвигом 1 на той же симпатии S.
Другой частный случай симпатии маршрутов — это так называемые симпатии кратных поколений. По определению симпатия кратных поколений кратностью k, построенная на симпатии S есть симпатия маршрутов длиной 0 и сдвигом k на этой симпатии. Ее элементами являются все элементы симпатии S. Областью интересов элемента симпатии кратных поколений является k–е поколение элемента симпатии S. В общем случае симпатия S0k распадается на k связных областей (если S включала одну связную область), однако за счет того, что некоторые элементы могут присутствовать в разных поколениях, симпатия может разделиться на меньшее число связных областей. В любом случае это число должно быть делителем числа k. Итак, симпатия кратных поколений S0k включает в себя те же элементы, что и симпатия S, т.е. строится на том же множестве, но ее элементы имеют другие области интересов.
Вернемся немного назад и поговорим о маршрутах. Вспомним, что маршрутом длины n называется упорядоченный набор из n+1 элементов симпатии S, из которых каждый последующий элемент входит в область интересов предыдущего. Мы говорим «набор», а не «множество», т.к. в множество элемент может входить только один раз, а на маршруте элемент может встречаться несколько раз. Говорят, что маршрут начинается в 1-м элементе этого набора, проходит через промежуточные элементы и заканчивается на последнем элементе набора. Допустимо также выражение: маршрут соединяет 1-й элемент набора с последним элементом набора.
Часть маршрута, в которой элементы следуют в том же порядке без пропусков, также является маршрутом. В этом случае говорят, что короткий маршрут входит в более длинный маршрут и называется его фрагментом. Кольцевым маршрутом называется маршрут, в котором первый элемент совпадает с последним элементом. Если в маршрут входит кольцевой маршрут, то говорят, что маршрут содержит кольцевой фрагмент. Два элемента в общем случае могут соединяться различными маршрутами различной длины. Среди маршрутов, соединяющих два элемента, из которых второй принадлежит области доступности первого, всегда есть один или несколько маршрутов наименьшей длины. Эта длина называется расстоянием от первого элемента до второго (или расстоянием между первым и вторым элементами). Расстояние между двумя элементами существует не всегда. Для конечных симпатий (т.е. для симпатий на конечных множествах) всегда существует маршрут, не содержащий кольцевых фрагментов и имеющий максимальную длину. Эта длина называется диаметром симпатии. Симпатии с бесконечным числом элементов также могут иметь конечный диаметр (хотя это и не обязательно). В симпатиях с конечным диаметром среди маршрутов между двумя элементами, второй из которых входит в область доступности первого, всегда есть один или несколько маршрутов без кольцевых фрагментов, имеющих максимальную длину. Эта длина называется максимальным путем между первым и вторым элементами.
Если два маршрута содержат один или несколько общих элементов, не составляющих фрагментов длины 1 и более, то говорят, что они пересекаются на этих элементах. Если два маршрута содержат один или более общих фрагментов, то говорят, что они совпадают на данных фрагментах или на данных участках. Заметим, что маршрут может совпадать на каком-либо участке с кольцевым маршрутом и в то же время не содержать кольцевых фрагментов. Если два маршрута являются фрагментами третьего маршрута, причем длина фрагмента третьего маршрута от начального элемента первого маршрута до начального элемента второго маршрута равна n, то говорят, что второй маршрут сдвинут относительно первого на n. Число n в этом случае может быть как меньше длины 1-го маршрута, так и больше ее. Если 2-й маршрут сдвинут относительно 1-го на n, то 1-й маршрут сдвинут относительно второго на −n. Если n=0, т.е. 2-й маршрут сдвинут на 0 относительно 1-го, то один из них является фрагментом другого. Еще раз обращу внимание на то, что в определение относительного сдвига двух маршрутов входит ссылка на 3-й маршрут, фрагментами которого первые два должны являться. Поэтому сдвиг определен не для любых двух маршрутов на данной симпатии, а только в том случае, если такой 3-й маршрут существует. В частности, если сдвиг n больше длины 1-го маршрута, то величина n в общем случае определена неоднозначно, т.к. длина фрагмента 3-го маршрута между концом 1-го маршрута и началом 2-го маршрута может быть различной в зависимости от выбора 3-го маршрута.
Симпатией маршрутов Snk на симпатии S называется симпатия, элементами которой являются маршруты длиной n на симпатии S, а в область интересов данного элемента входят все маршруты симпатии S длины n, сдвинутые относительно маршрута-элемента на величину k. Это повторение определения, данного ранее, но через сдвиг маршрутов. Кроме того, в новом определении нет ограничения на величину сдвига — она может быть как положительной, так и нулевой, и отрицательной. Отметим, что симпатии маршрутов с нулевым сдвигом Sn0 не имеют связей между элементами (не считая самолюбования) и, по-существу, являются просто множествами маршрутов длины n. Симпатии маршрутов с отрицательным сдвигом являются обратными симпатиями по отношению к симпатиям маршрутов с положительным сдвигом: Sn,-k= S'nk. В частности, S0,-1= S'01= S' — обратная симпатия к симпатии S.
Вернемся к симпатиям интересов n–го порядка. Мы уже отмечали, что Sn= Sn1, т.е. симпатии интересов n–го порядка — это симпатии маршрутов длины n со сдвигом 1. Ясно, что при переходе к симпатии интересов длина любого маршрута, начинающегося истоком и кончающегося тупиком, сокращается на 1. Кольцевой же маршрут в симпатии интересов не изменяет своей длины. Поэтому, если исходная симпатия конечна и не имеет кольцевых маршрутов, то длина всех маршрутов от истоков до тупиков, а значит и диаметр симпатии интересов n–го порядка, взятой от данной симпатии, уменьшается на n. Отсюда следует вывод: если порядок симпатии интересов превышает диаметр исходной симпатии, не содержащей кольцевых маршрутов, то такая симпатия интересов пуста, т.е. не имеет элементов.
По-иному обстоит дело, если симпатия имеет кольцевые маршруты. В этом случае длина чисто линейных маршрутов от истока до тупика, т.е. маршрутов, не имеющих ни одного общего элемента с кольцевыми маршрутами, при каждом переходе к симпатии интересов сокращается на единицу. Длина маршрутов, имеющих общий фрагмент с кольцевым маршрутом, но начинающихся с истока и кончающихся тупиком, также сокращается при каждом переходе к симпатии интересов, но к ней периодически добавляется длина кольца, так что, если такой маршрут окажется маршрутом максимальной длины, то диаметр симпатии будет совершать колебания при увеличении порядка симпатии интересов с периодом, равным длине кольцевого маршрута. Длина маршрута, начинающегося или кончающегося на кольце (и не имеющего кольцевых фрагментов), в симпатии интересов не изменяется. Наконец, если маршрут и начинается, и кончается на кольце, то длина его (т.е. максимальная длина без кольцевых фрагментов) с каждым переходом к симпатии интересов увеличивается на единицу. Если такая структура присутствует в симпатии, то с увеличением порядка симпатии интересов рано или поздно ее диаметр начнет расти.
Симпатия интересов в качестве элементов использует связи исходной симпатии. Каждый элемент исходной симпатии имеет [Mi] + [M'i] связей (а при наличии самолюбования [Mi] + [M'i] − 1 связей, т.к. самолюбование учитывается и в [Mi], и в [M'i]). Через элемент исходной симпатии проходит [Mi] × [M'i] маршрутов длины 2, для которых этот элемент является промежуточным. Эти маршруты соответствуют связям в симпатии интересов. Таким образом, каждая связь исходной симпатии превращается в элемент симпатии интересов, а каждый элемент исходной симпатии — в [Mi] × [M'i] связей симпатии интересов.
Можно ли, зная структуру симпатии интересов, восстановить исходную симпатию? Сразу можно сказать, что однозначно это сделать нельзя. Так, например, три следующие симпатии

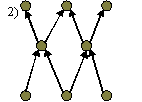
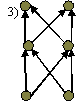
имеют одну и ту же симпатию интересов:
 .
.
Т.е симпатия интересов 4 имеет не менее трех вариантов исходной симпатии (на самом деле их 9, если не учитывать варианты с изолированными элементами). Другой вопрос: любая ли симпатия является симпатией интересов какой-либо другой симпатии? Ответ на этот вопрос тоже отрицательный. Так, например, не существует симпатии, для которой симпатия

была бы симпатией интересов. Тогда встает следующий вопрос: как по структуре симпатии определить, является ли она чьей-нибудь симпатией интересов или нет? Прежде всего, в симпатии интересов если два элемента имеют пересекающиеся области интересов, то эти области интересов полностью совпадают. То же самое можно сказать и о кругах поклонников — для любых двух элементов они либо не пересекаются, либо совпадают. Т.е. вся симпатия распадается на набор непересекающихся множеств, являющихся областями интересов элементов других множеств — множеств поклонников, которые также не пересекаются. То есть симпатия интересов всегда имеет четко организованную структуру, она всегда разбита с одной стороны на «творческие коллективы», с другой стороны на «фан-клубы», причем каждый элемент такой симпатии не может находиться ни в двух «творческих коллективах», ни в двух «фан-клубах» одновременно, а члены каждого «фан-клуба» проявляют интерес только к одному «коллективу». Заметим, что среди тех и других множеств может быть какое-то число пустых множеств, которые также (что естественно) не пересекаются с другими множествами, в том числе и пустыми. Именно неопределенность числа множеств и порождает неоднозначность исходных симпатий для данной симпатии интересов.
Итак, для того, чтобы данная симпатия была симпатией интересов какой-либо другой симпатии, необходимо и достаточно, чтобы области интересов любых двух элементов этой симпатии либо полностью совпадали, либо не пересекались. При этом множество элементов симпатии разбивается на ряд непересекающихся множеств интересов элементов с одной стороны и на ряд непересекающихся множеств поклонников с другой стороны, причем между множествами интересов и множествами поклонников имеется взаимно однозначная связь такая, что любой элемент из множества поклонников является поклонником любого элемента из связанного с ним множества интересов. Такая связь и есть то, во что превращается элемент симпатии при переходе к симпатии интересов. Таким образом, если мы хотим восстановить исходную симпатию S, имея только симпатию интересов S1, мы должны сделать следующее:
Выделить области интересов всех элементов S1. Они должны либо совпадать, либо не пересекаться (иначе данная симпатия не является симпатией интересов никакой симпатии).
Выделить области поклонников всех элементов S1. Они также должны либо совпадать, либо не пересекаться.
Установить связи между множествами поклонников и множествами интересов (естественно, количество множеств интересов и количество множеств поклонников всегда совпадает).
Заменить каждую связь между множеством интересов и множеством поклонников S1 на элемент симпатии S. Этот элемент будет иметь столько интересов, сколько элементов в соответствующем множестве интересов, и столько поклонников, сколько элементов в соответствующем множестве поклонников.
Для каждого элемента симпатии S рассматриваем каждый элемент симпатии S1, входящий в соответствующее множество интересов. Он будет соответствовать связи данного элемента симпатии S с тем элементом этой же симпатии, который содержит тот же элемент симпатии S1 в соответствующем ему множестве поклонников.
Дописываем к связям, соответствующим элементам S1, не входящим ни в одно множество интересов, необходимое число истоков в S, а к не входящим ни в одно множество поклонников — необходимое число тупиков в S.
Добавляем в полученную симпатию S произвольное число изолированных элементов.
Поясним сказанное примером. Пусть мы имеем симпатию S1 со следующей структурой:

Разбиваем множество элементов симпатии S1 на множества интересов и множества поклонников и связи между ними считаем элементами симпатии S (обозначены на схеме заглавными буквами).
| Mi |
| |||||||
| ||||||||
| M'i |
|
Восстанавливаем всю «промежуточную» структуру симпатии за исключением «концевых» элементов, т.е. истоков и тупиков. К таким элементам ведут связи, соответствующие элементам симпатии S1, не входящим ни в одно множество интересов или ни в одно множество поклонников (выделенные серым фоном элементы в нашем примере).

Количество тупиков в нашем примере определяется однозначно, т.к. имеется лишь одна свободная связь (интерес) a7. Мы можем поставить сюда тупик A7. А вот количество истоков может быть 1 или 2 (связи a8 и a10). Можно поставить один элемент (A8) или два (A8 и A9). В зависимости от этого мы имеем два варианта исходной симпатии S:


Диаметр симпатии S в этом примере равен 7 (максимальный маршрут A9A1A2A3A4A5A6A7), а диаметр симпатии S1 равен 6 (a10a9a1a2a3a6a7). 7 — 6 = 1. Так и должно быть, т.к. здесь диаметр определяется некольцевым маршрутом. В то же время длина кольцевых маршрутов не изменилась |A2A4A5A2| = 3, |a4a5a3a4| = 3, |A2A3A4A5A2| = 4, |a4a1a2a3a4| = 4.
Ни один из полученных вариантов симпатии в нашем примере не является в свою очередь симпатией интересов какой-либо другой симпатии. В самом деле, M2 = {A3, A4}, M3 = {A4} — данные два множества пересекаются, но не совпадают. То же самое можно сказать и о множествах M1, M5 и M8.
Сколько вариантов исходной симпатии можно построить для данной симпатии интересов? Ответ на этот вопрос зависит от количества концевых связей при построении исходной симпатии, т.е. от количества тупиков и истоков в симпатии интересов. Это количество тупиков и истоков определяет максимально возможное количество тупиков и истоков в исходной симпатии. Минимально же возможное количество тупиков равно максимальному количеству тупиков в симпатии интересов, присутствующих в одной области интересов. Минимальное количество истоков равно максимальному количеству истоков в симпатии интересов, присутствующих в одном круге поклонников. Количество вариантов в каждом конкретном случае зависит от распределения тупиков и истоков по связанным с ними элементам и даже от симметрии структуры симпатии, что не позволяет дать конкретные рекомендации на все случаи жизни.
Заметим еще, что при переходе от симпатии интересов к исходной симпатии мы можем добавить к ней произвольное количество изолированных элементов (что увеличивает количество вариантов до бесконечности).
Фу! Наконец-то я закончил эту большую тему — симпатии интересов. А впереди еще много и симпатичного, и интересного.