| Теория симпатий> | Письмо 1 — введение в теорию Письмо 1 — симпатии интересов Письмо 1 — классификация Письмо 2 — согласия Письмо 2 — размерность | Архив статьи |

| Теория симпатий> | Письмо 1 — введение в теорию Письмо 1 — симпатии интересов Письмо 1 — классификация Письмо 2 — согласия Письмо 2 — размерность | Архив статьи |

Женя! Тебе, наверное, уже надоели мои постоянные возвращения назад, к азам. Мне самому надоели. Но что ж поделаешь, не получается все сразу предусмотреть. Вот и сейчас хочу вернуться к определению линии. Я определил ее как согласие, в котором каждый элемент имеет не более двух связей. И получил 4 типа связной линии: бесконечная линия, луч, отрезок и замкнутая линия. Если не считать, конечно, изолированной точки. Сейчас же мне представляется более удобным считать линией согласие, в котором каждый элемент имеет ровно две связи. По этому определению имеем только два типа линии, отличающиеся числом элементов. При бесконечном числе точек имеем бесконечную линию. При конечном числе точек — замкнутую линию. А такие объекты, как луч и отрезок нельзя считать линиями, т.к. кроме чисто линейных точек (с двумя взаимностями) они имеют точки с одной связью (концевые или краевые точки). Отрезок и луч определим, как связные усечения линии (или фрагменты линии).
Такое определение позволяет логично провести аналогию к определению фрагмента поверхности, фрагмента 3-мерного согласия и т.д.
Фрагментом поверхности назовем связное усечение поверхности, локально плоское во всех точках кроме множества краевых точек, усечение на котором образует одну или несколько линий. В этом случае будем говорить, что фрагмент поверхности ограничен одной или несколькими линиями. В каждой из краевых точек фрагмент поверхноти не является локально плоским, т.к. окружение этих точек не образует линии, а образует отрезок с концевыми точками, являющимися также краевыми точками фрагмента поверхности.
Фрагментом 3-мерного согласия называется связное усечение на 3-мерном согласии, ограниченное одной или несколькими поверхностями. Слово «ограниченное» понимается в том смысле, что точки, принадлежащие ограничивающей поверхности, не являются локально трехмерными, т.к. их окружение образует не поверхность, а фрагмент поверхности, ограниченный линией, причем точки этой линии также принадлежат к этой ограничивающей поверхности.
Почему в обоих определениях (фрагмента поверхности и фрагмента 3-мерного согласия) я употребил слова «одной или несколькими»? Это на тот случай, если фрагмент кроме «внешнего» контура имеет еще «внутренние» контуры отверстий (для поверхности) или пустот (для 3-мерного фрагмента). То есть здесь сразу учитывается топология фрагментов.
И, наконец, почему я требую, чтобы фрагмент поверхности был ограничен линиями, а фрагмент 3-мерного согласия — поверхностями? Потому что можно построить усечения, ограниченные черт те чем, например, древовидные структуры, которые близко не лежали с поверхностями или 3-мерными согласиями.
Понятия линии, поверхности, 3-мерного согласия и вообще n-мерного согласия закладывают основы для создания дискретной геометрии, дискретной топологии и прочих дискретных наук, известных нам только в непрерывном варианте.
А теперь вновь вернемся назад, чтобы определить размерность для более общего случая. Дело в том, что согласия не ограничиваются только линиями, поверхностями, 3-мерными и т.д. согласиями и их фрагментами, а могут представлять собой более сложные структуры. Например, такое согласие:

Если даже не считать область IV, состоящую из изолированных элементов, то области I, II, III составляют связную область, не являющуюся ни линией, ни поверхностью, ни 3-мерным согласием, ни их фрагментом. В то же время область I (вернее, усечение на области I) — это фрагмент 3-мерного согласия (объемноцентрированный октаэдр), область II — отрезок, т.е. фрагмент линии, а область III — полноправная поверхность. Т.е. разные части этого согласия имеют разную размерность. Минимальной частью согласия, в которой можно определить размерность, является точка. Ведь и линию, и поверхность, и 3-мерное согласие мы определяли через свойства точки (2 связи для линии, локальная плоскостность и локальная 3-мерность для двух других случаев).
Начнем с нулевой размерности. Точка согласия, не имеющая соседей (изолированный элемент) имеет нулевую размерность.
Если же точка имеет соседей, то размерность этой точки больше нуля. Для того, чтобы определить размерность точки, надо рассмотреть усечение на окрестности этой точки (в дальнейшем для краткости вместо слов «усечение на окрестности» будем говорить просто «окрестность»). Если окрестность состоит только из изолированных точек, т.е. никакие две точки из окрестности не связаны между собой, то размерность в такой точке равна 1. Итак, одномерной называется точка, усечение на окрестности которой состоит из точек размерности 0. Заметим, что одномерная точка может иметь любое число соседей (не обязательно 2), главное, чтобы эти соседи были и чтобы они не были связаны между собой. В общем случае согласие, состоящее только из одномерных точек, представляет собой сложную разветвленную структуру. В ней возможны круговые маршруты, не должно только присутствовать ни одного элементарного треугольника, т.е. треугольника со стороной, равной 1, т.к. точки, входящие в такой треугольник, имеют связанных между собой соседей, и размерность этих точек больше 1.
Размерность 2 имеют точки, усечение на окрестности которых содержит точки размерности 1 и, возможно, точки размерности 0.
Общее определение размерности точки:
Точка имеет размерность n, если максимальная размерность точек усечения на окрестности этой точки равна n-1. Размерность изолированной точки равна 0.
Все рассмотренные нами усечения (фрагменты) линии, поверхности, 3-мерного согласия (кроме вырожденных) имели ту же размерность во всех точках, что и само согласие. Для последнего согласия (см. предыдущую диаграмму) все точки области I имеют размерность 3, причем центральная точка локально трехмерна, а остальные — граничные точки трехмерной области. Только точка, связанная с областью II, имеет более сложное окружение, состоящее из фрагмента поверхности и изолированной точки. Тем не менее, ее размерность — 3. Точки области II одномерны. Точки области III двухмерны, причем все кроме точки, связанной с областью II, локально плоски, а последняя имеет окрестность, состоящую из линии и изолированной точки. Точки области IV имеют размерность 0.
В определении размерности согласия имеется некоторая двойственность, касающаяся минимальных конфигураций. Рассмотрим, например, линию (конечно, замкнутую), состоящую из n точек. Размерность линии, как и размерность всех ее точек, равна 1 и не зависит от n. Однако, если мы сделаем n равным минимально возможному значению, т.е. 3, то размерность точек окажется равной 2. В самом деле, окрестность каждой точки состоит из двух связанных точек, т.е. имеет размерность 1, а значит размерность самой точки равна 2. Т.е., уменьшив линию до минимума, мы превратили ее в фрагмент поверхности. Этот фрагмент состоит из трех краевых точек, образующих краевую линию, и не содержит ни одной полноценно двумерной точки (т.е. имеющей окрестность в виде линии — локально плоской). Размерность краевой точки фрагмента поверхности, как мы знаем, равна 2. Размерность краевой точки в усечении на краевом множестве есть размерность линии и должна равняться 1. Но в минимальном случае усечение на краю совпадает с самим фрагментом поверхности и размерность его точек есть 2.
Точно так же, тетраэдр есть минимальная поверхность, но одновременно он является фрагментом пространства, (т.е. 3-мерного согласия), и размерность точек тетраэдра равна 3. Этот фрагмент также целиком состоит из краевой поверхности и не имеет ни одной «полноценно» трехмерной точки.
Если мы попытаемся добавить в центр тетраэдра такую «полноценную» точку, сделав весь тетраэдр ее окрестностью, то и все остальные точки станут также «полноценно» пространственными, т.е. мы получим 3-мерное согласие. Но, т.к. точки исходного тетраэдра имели размерность 3, то точки полученного согласия будут иметь размерность 4, т.е. мы имеем фрагмент 4-мерного согласия, ограниченный 3-мерным согласием, в которое входят все точки фрагмента.
Таким образом, минимальные n-мерные согласия всегда являются фрагментами n+1-мерных согласий, и все их точки имеют размерность n+1.
Рассмотрим случай, когда окрестность точки (понимаемая как усечение на множестве соседних точек) многосвязна. Тогда каждая связная область окрестности определяет свою размерность точки. По нашему определению размерность точки на 1 больше максимальной из размерностей точек окрестности. Но связные области, состоящие из точек, чья размерность меньше максимальной, также вносят свой вклад в свойства точки. Будем называть такие точки (т.е. точки, имеющие многосвязную окрестность) точками соприкосновения. В этих точках соприкасаются области согласия, имеющие (по крайней мере, вблизи этих точек) обособленные структуры и, возможно, даже разные размерности.
Можно ввести формальную операцию разделения согласия, заменяющую каждую точку соприкосновения несколькими точками, имеющими односвязные окрестности, каждая из которых является связной областью окрестности исходной точки. Не следует проводить разделения по точкам окрестности с размерностью 0, т.е. по изолированным точкам окрестности, если таких точек ровно 2 и кроме них окрестность не содержит других точек, т.к. иначе мы разобьем все линейные структуры на элементарные отрезки, что может только затруднить исследование конкретного согласия. А в целом разделение согласия по точкам соприкосновения может помочь лучше понять его структуру. В частности, области с разными размерностями при этом окажутся отдельными связными областями.
Отметим также, что разделение согласия — это одна из обратных операций по отношению к сокращению, причем, что несколько парадоксально, и ту, и другую мы ввели для того, чтобы упростить структуру симпатии и облегчить ее исследование.
Еще более сложный вариант может возникнуть, когда окрестность точки сама содержит (нелинейные) точки соприкосновения. В этом случае имеет смысл говорить о линиях соприкосновения или их фрагментах, проходящих через данную точку и точку соприкосновения из окрестности. Если же окрестность содержит точки, соединенные в линию соприкосновения, то мы имеем дело с поверхностью соприкосновения трех- или более- мерных областей.
Теперь для ясности поговорим немного об очевидных вещах, упомянутых в предыдущих рассуждениях. Мы предлагали не проводить разделения по линейным точкам (т.е. тем, у которых окрестность состоит из двух изолированных элементов). Такие точки также являются точками соприкосновения, например, левой части линии (или ее фрагмента) с правой частью. Разделение по таким точкам разобьет всю линию на единичные отрезки. Конечно, удобнее иметь дело с целой линией или фрагментом, лишь отделив его на концах от других структур, т.е. линий, поверхностей и т.д. Если же точка одномерна, но ее окрестность состоит из 3 или более изолированных точек, то, в принципе, можно было бы разбить эти точки на пары и считать, что в данной точке имеется пересечение какого-то количества линий и, возможно, ответвление линейной структуры (если число точек окрестности нечетно). Но разбиение на пары вносит элемент произвола, и разделение по «парному» принципу приводит к неоднозначности. Необходимо проводить разделение в таких одномерных точках по каждому из направлений для всех точек окрестности, этим мы избежим неоднозначности и сделаем равноправными все направления.
Определяя линию соприкосновения, мы говорили, что она проходит через нелинейные точки соприкосновения из окрестности. Через линейные точки соприкосновения также можно провести линию, и по этой линии будут соприкасаться части поверхности. Но части поверхности соприкасаются по любой линии, проведенной на поверхности, эта линия не есть линия соприкосновения разных объектов, так же как и линейная точка не есть точка соприкосновения разных объектов, а просто точка, где сходятся части одной и той же линии.
Для поверхности соприкосновения мы не оговаривали чисто поверхностные линии соприкосновения, т.к. предыдущим определением мы их уже исключили из понятия «линия соприкосновения». Это можно было бы сделать еще раньше, исключив из понятия «точка соприкосновения» линейную точку, но на этапе точки это показалось мне несколько искусственным.
Любое связное согласие либо имеет все точки одной и той же размерности, либо может быть разбито на области, состоящие из точек разных размерностей, но совпадающих внутри областей, причем эти области связаны через точки, линии и т.д. соприкосновения (это, конечно, требует доказательства, но это так).
Таким образом, изучив окрестность каждой точки согласия, мы можем не только определить ее размерность, но и сказать, является ли она точкой соприкосновения каких-либо областей с определенными размерностями, либо, возможно, входит в линию, поверхность или другую структуру соприкосновения таких областей. При необходимости, проведя разделение по всем точкам, линиям и т.д. соприкосновения мы можем разделить согласие на отдельные области, имеющие более простую структуру.
Разделение по линии соприкосновения производится следующим образом. Окрестность каждой точки линии соприкосновения разделяется по точкам соприкосновения. В результате точка линии соприкосновения превращается просто в точку соприкосновения, т.е. ее окрестность становится многосвязной. Поэтому после разделения окрестностей становится возможным разделение по самим точкам линии.
Разделение по поверхности соприкосновения предполагает разделение окрестностей всех точек этой поверхности по линии соприкосновения, а затем разделение самих точек поверхности соприкосновения, как простых точек соприкосновения.
Назовем согласие, все точки которого имеют одинаковую размерность, равномерным («равно-мерным»). Соответственно, если согласие содержит точки разной размерности, оно будет называться неравномерным. Размерностью равномерного согласия будем считать размерность его точек.
Справедливо следующее утверждение: число точек равномерного согласия всегда больше его размерности. Для размерности 1 это очевидно. Для большей размерности доказывается по индукции (рассматривается окрестность точки размерности n+1, которая является согласием размерности n, т.е. содержит не менее n+1 точек).
Для неравномерного согласия не только общее число точек больше максимальной размерности точек, но число точек с максимальной размерностью больше значения размерности. Что касается числа точек с размерностями, меньшими максимальной, то оно может быть любым. Например, в согласии:
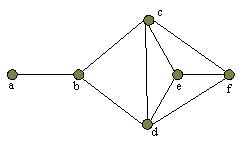
содержится 6 точек. Из них 4 (c, d, e, f) имеют максимальную размерность, равную 3. Точка b имеет размерность 2, а точка a — размерность 1. При этом точка b является точкой соприкосновения одномерной области (ab) с двумерной bcd), а отрезок cd — линией соприкосновения двумерной области (bcd) с трехмерной (cdef). Эти области становятся связными областями после разделения согласия по точке соприкосновения b и линии соприкосновения cd:

Очевидно, что любая одномерная точка всегда связана хотя бы с одной другой точкой, т.е. входит в элементарный отрезок. Любая двухмерная точка всегда содержит элементарный отрезок в своем окружении, т.е. входит в элементарный треугольник. Любая трехмерная точка входит в тетраэдр. И т.д. Вообще, всякая n-мерная точка является точкой минимального (элементарного) n-мерного фрагмента. Минимальной частью (усечением) n-мерного согласия, сохраняющей свойства n-мерности всегда является минимальный n-мерный фрагмент. Для n=1 это единичный отрезок, n=2 — элементарный треугольник, n=3 -элементарный тетраэдр и т.д. Количество элементарных n-мерных фрагментов, содержащихся в согласии является аддитивной мерой согласия по отношению к n-му измерению. Мы будем называть это количество в общем случае количеством n-мерных ячеек.
Количество нульмерных ячеек — это просто количество элементов согласия, т.е. его мощность.
Количество одномерных ячеек — это количество связей в согласии, а для равномерного одномерного согласия — длина.
Количество двумерных ячеек — это количество элементарных треугольников, а для двумерного согласия — площадь.
Количество трехмерных ячеек для трехмерного согласия характеризует его объем. Дл четырехмерного согласия количество 4-мерных ячеек есть гиперобъем и т.д.
Надо отметить, что любое n-мерное согласие характеризуется не только количеством n-мерных ячеек, но и количеством ячеек всех меньших измерений вплоть до нуля. Т.е., например, трехмерный фрагмент характеризуется не только объемом, но и своими «внутренними» площадью, длиной и мощностью. Этим дискретные многомерные объекты отличаются от непрерывных. Для непрерывного тела мы можем указать только объем. Поверхность может быть указана только внешняя, т.е. краевая, которая не имеет отношения к количеству 2-мерных ячеек в дискретном случае (в дискретном случае тоже есть краевая поверхность 3-мерного фрагмента, но это только часть всей «внутренней» площади дискретного тела).
Например, рассмотренное выше неравномерное согласие имеет мощность 6, длину 9, площадь 5 и объем 1. После разделения согласия увеличивается только количество объектов, по которым производилось разделение. Так для разделенного согласия мощность увеличилась до 9, длина до 10, площадь и объем не изменились (5 и 1), т.к. по 2- и 3-мерным фрагментам разделения не производилось.
Интересно посмотреть, сколько ячеек меньших размерностей содержит n-мерная ячейка. Оказывается, количество таких ячеек выражается биноминальными коэффициентами
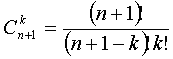 ,
,
где k — размерность ячеек. Так, например, 5-мерная ячейка содержит 6 четырехмерных ячеек, 15 трехмерных, 20 двухмерных, 15 одномерных и 6 точек.
Рассмотрение многомерных дискретных структур намного проще, чем рассмотрение многомерных непрерывных объектов, чисто в психологическом плане. Трудно себе представить тессеракт (4-мерный куб), тогда, как, например, 5-мерная ячейка, для которой мы считали число ячеек меньших измерений, легко изображается на бумаге и не требует титанических усилий воображения:
 .
.
Можно и далее развивать дискретную геометрию, ввести понятия прямой, плоскости, угла, рассмотреть фигуры и тела для согласий разных конфигураций, вычислить соотношения между их элементами, их площади, объемы и т.д. Дискретная геометрия так же неисчерпаема, как и непрерывная (ой, кажется, я сказал что-то великое). Но оставим все это на будущее и рассмотрим несколько иные аспекты теории согласий.
Согласием взаимностей, построенным на согласии S, назовем согласие, элементами которого являются взаимности согласия S, а в окружение каждого элемента входят все отличные от самого элемента взаимности, относящиеся к двум элементам согласия S, образующим эту взаимность.
Ага! Ведь это то же самое, что и симпатия интересов, только в применении к согласию! — наверное воскликнул Евгений Григорьевич, прочитав предыдущий абзац. Если, конечно, у него хватило терпения вообще дочитать до этого места. Но будем думать, что именно ты, Женя, и дочитал, и воскликнул. Я отвечу: Да! Ты прав. Но именно поэтому я и начну с отличий согласия взаимностей от симпатии интересов и, конечно, со связи между ними.
Рассмотрим такое простенькое согласие:
 .
.
Это элементарный треугольник. Рассмотрим его, как симпатию
 .
.
и возьмем от него симпатию интересов:
 .
.
Как видим, симпатия интересов от нашего согласия вовсе не похожа на согласие. А вот согласие взаимностей согласно нашего определения:
 .
.
Мы видим, что симпатия интересов от согласия содержит пары элементов, связанные взаимностями, и, чтобы перейти от симпатии интересов к согласию взаимностей, необходимо сократить эти пары, т.е. заменить их единичными элементами. Таким образом, согласие взаимностей получается из исходного согласия путем перехода к симпатии интересов и сокращения всех пар элементов, связанных взаимностями.
Учитывая это отличие, можно дальнейшие вопросы, связанные с согласиями взаимностей, развивать совершенно аналогично тому, как мы это делали для симпатий интересов. В частности, так же вводятся согласия взаимностей n-го порядка, согласия маршрутов длины n со сдвигом k, и между ними существуют аналогичные зависимости.
И, наконец, об операции, применимой к любой симпатии, — операции, превращающей симпатию в согласие. Назовем эту операцию согласованием симпатии, а заключаться она будет в следующем. Для каждого элемента ai просматривается область его интересов и каждому элементу aj, входящему в область интересов элемента ai, в его область интересов вписывается элемент ai (если его там нет). Если проще, то каждая направленная связь симпатии заменяется на двойную, т.е. на взаимность. Тем самым осуществляется вековая мечта всех влюбленных: предметы нашего обожания втюриваются в нас по уши, и на планете наступает рай земной, вечная весна и прочая идиллия. Конечно, при этом все общество теряет неудовлетворенность, направленность, импульс к развитию, время останавливается, и приходит вечный, многомерный и совершенно бессмысленный бардак, т.е., в нашей терминологии, «согласие» или, как говаривал один уже забываемый временами деятель, «консенсус». Но в смысле математики такая идиллическая операция может сослужить неплохую службу, например, помочь в исследовании топологии симпатии и в некоторых других случаях, когда направленность связей роли не играет. Самый первый пример, который приходит в голову — это выделение связной области в симпатии.
Кстати очень красиво согласование выглядит в выражениях родственной логики: согласование есть объединение симпатии с ее обратной симпатией. Мне это сильно напоминает поговорку «крайности сходятся», смысл которой практически совпадает со смыслом «родственно-логической» трактовки: наиболее крепкая семья (согласие) получается при браке (объединении) наиболее отличающихся друг от друга индивидов (прямая и обратная симпатия). Ну как тут не порадоваться удачному выбору терминов!
На этом, Женя, заканчиваю сие малохудожественное повествование. Надеюсь, некоторых своих целей это письмо достигло. Одна из них — заинтересовать тебя математической теорией, выполненной на стыке с демагогией чувств. Конечно, я и не пытался оцифровать движения души, скорее, наоборот, была попытка вдохнуть душу в такой сухой предмет, как теория множеств. А другая цель — доверить бумаге продукт устного (даже не устного, а мысленного, поскольку вслух об этом никому не сообщалось) творчества, ведь бумага более долговечна, чем наша память. А в моих построениях, думаю, согласишься, что-то есть из тех вещей, которые стоит сохранить надолго.
12.02.99
Белюченко Николай.