Теория симпатий>

Письмо 1 — введение в теорию Письмо 1 — симпатии интересов Письмо 1 — классификация Письмо 2 — согласия Письмо 2 — размерность

Архив статьи

Теория симпатий — письмо 2 — согласия

Евгений Григорьевич!

Наконец-то возвращаюсь к неоконченной теме теории симпатий. Просто кончилась моя месячная вахта, дома было не до того, а здесь на новой вахте заели другие дела.

Больше не для тебя, а для себя напомню, что предыдущее пухлое письмо было посвящено исследованию математических объектов, которые я назвал симпатиями. Это множества, в которых для каждого элемента определено подмножество этого множества, называемое областью интересов. Были определены такие понятия, как обратная симпатия, область доступности или будущее, круг поклонников, область популярности или прошлое элемента, маршрут, расстояние между элементами, связность симпатии, диаметр симпатии, подсимпатия, связная область, кольцевой маршрут. Были определены такие операции на симпатиях, как сокращение симпатии, раскольцевание симпатии, получение симпатии интересов n-го порядка, получение симпатии маршрутов длины n со сдвигом k, установлена связь между некоторыми из этих операций и условия для существования обратных операций (для симпатий интересов). Была проведена классификация симпатий и рассмотрены некоторые симпатии как общего вида, так и разных классов. Так симпатии делятся на конечные и бесконечные, а последние на симпатии с конечным числом элементов в областях интересов и бесконечным числом. Кроме того выделены и рассмотрены однородные и однозначные симпатии, в частности, функции, симпатии с кольцевыми маршрутами и без них, и, наконец, согласия, т.е. симпатии с двунаправленными связями. Вот как раз на согласиях и прервался ход моей мысли, и логично было бы продолжить сие повествование именно с них. Однако вернусь к более ранней и общей теме, т.к. в свое время я ее недостаточно осветил. А именно к подсимпатиям.

Подсимпатией данной симпатии является симпатия на подмножестве множества элементов данной симпатии, причем области интересов всех элементов подсимпатии совпадают с областями интересов тех же элементов основной симпатии. Ясно, что не любое подмножество множества элементов симпатии может быть подсимпатией. В частности, связная область симпатии всегда является подсимпатией. Также подсимпатией буде будущее, т.е. область доступности любого элемента. Обратные симпатии к подсимпатии не всегда являются подсимпатиями симпатии, обратной к основной. Так, например, если подсимпатия строится на связной области, то обратная к ней симпатия будет подсимпатией обратной к основной симпатии. А вот обратная подсимпатия к будущему элемента не обязательно должна быть подсимпатией обратной основной симпатии. В общем случае подсимпатия всегда является объединением областей доступности какого-то количества элементов основной симпатии.

Однако, если не требовать совпадения областей интересов элементов основной симпатии и ее части, а оставить в областях интересов части только ссылки на элементы, входящие в эту часть, можно получить из данной симпатии целый класс симпатий, построенных на подмножествах основного множества и частично сохраняющих структуру основной симпатии. Мы назвали такие симпатии усечениями основной симпатии.

Усечением (S_y) симпатии (S) называется симпатия, множество элементов (M_y) которой является подмножеством множества элементов (M) симпатии (S), а области интересов (M_yi) являются пересечениями областей интересов (M_i) тех же элементов с множеством элементов (M_y) усечения. При таком определении на любом подмножестве основного множества можно построить усечение, причем все связи внутри усечения будут повторять связи основной симпатии, из связей основной симпатии отбрасываются лишь те, которые ведут к элементам, не входящим в подмножество, т.е. «наружу» по отношению к усечению. Т.к. подсимпатия является частным случаем усечения, то симпатия, обратная подсимпатии, всегда является усечением (т.к. очевидно, что симпатия, обратная усечению есть усечение обратной симпатии) обратной симпатии. Подсимпатии можно разбить на двусторонние (т.е. те, для которых и обратные симпатии есть подсимпатии S') и односторонние (например, будущее элемента). Можно доказать, что двусторонняя подсимпатия всегда строится на множестве, составляющем одну или несколько связных областей основной симпатии.

Следует отличать усечение и симпатию, являющуюся результатом сокращения симпатии. Усечение — это часть симпатии, а при сокращении мы получаем «модель» симпатии, ее более простой вариант, в котором «неинтересная» часть заменена на абстрактный элемент с сохранением всех его внешних связей. Только в тривиальном случае, когда усечением является сама симпатия, а сокращается (т.е. заменяется на абстрактный) только один элемент, усечение может совпасть с результатом сокращения.

Дадим также определение родственных симпатий. Родственными симпатиями называются симпатии, построенные на одном и том же множестве. Понятие родственных симпатий позволяет ввести парные операции на множестве симпатий, такие, например, как объединение двух симпатий ( когда области интересов элементов объединяются) или пересечение (когда в область интересов результирующей симпатии включаются только интересы, присутствующие в обеих пересекающихся симпатиях). Следует сразу же подчеркнуть отличие операций с родственными симпатиями от одноименных операций на множествах — там объединяются или пересекаются множества элементов, а для родственных симпатий — только области интересов. Родственными всегда являются прямая и обратная симпатии. Таким образом, на родственных симпатиях оказываются определенными базовые логические операции (и, или, не), что позволяет организовать родственную логику. Впрочем, ничего особо нового от такой логики ожидать не приходится.

А теперь перейдем к согласиям, т.е. к симпатиям, у всех элементов которых области интересов совпадают с кругами поклонников. Все двусторонние связи в согласиях мы учитываем только один раз, так что под словом «связь» в дальнейшем будем понимать пару связей, составляющих взаимность. На диаграммах взаимность будет изобрадаться линией без стрелок.

Строго говоря, каждая такая связь является кольцевым маршрутом. Поэтому на согласиях мы будем говорить не о кольцевых маршрутах, а о круговых маршрутах, составленных из однократно пройденных взаимностей. Область интересов или круг поклонников для согласий будем называть общим словом «окружение» (если ты помнишь, для симпатий в общем виде мы так называли объединение области интересов с кругом поклонников — так что терминология согласий не противоречит общей). Элементы, входящие в окружение данного элемента будем называть соседними.

Если в общем случае симпатия является времениподобной структурой, что отражается в терминологии: прошлое, будущее, поколения, то частный случай согласия явно теряет всякое подобие со временем — здесь прошлое совпадает с будущим, поколения — это множества элементов, расположенных на одинаковых расстояниях от данного, т.е. нечто похожее на окружности или сферы. Поэтому для согласий больше подходят аналогии с пространством, геометрией, и названия для некоторых специальных понятий мы в дальнейшем будем брать именно оттуда.

Согласием линейного типа назовем согласие, в котором каждый элемент имеет не более двух соседей. Согласие линейного типа разбивается на связные области, называемые линиями. Ясно, что линия может иметь не более двух элементов, имеющих только одну взаимность (концевых элементов). Существует 4 типа линий:

1. Линия с конечным числом элементов без концевых элементов — замкнутая линия.

2. Линия с бесконечным числом элементов без концевых элементов — бесконечная линия.

3. Линия с бесконечным числом элементов, содержащая один концевой элемент — луч.

4. Линия с конечным числом элементов, два из которых концевые — отрезок.

Луч и отрезок являются усечениями бесконечной линии (в дальнейшем мы уточним определение линии и будем называть луч и отрезок фрагментами линии в отличие от «настоящей» линии, не имеющей концов). Возможны и другие усечения бесконечной линии — наборы лучей, отрезков и изолированных элементов, причем лучей может быть не более двух, а количество отрезков и изолированных элементов в наборе не ограничивается.

Усечения луча — не более одного луча и неограниченное количество отрезков и изолированных элементов.

Усечениями отрезка может быть только ограниченное число отрезков и изолированных элементов.

Усечения замкнутой линии набор ограниченного числа отрезков и изолированных элементов.

Для линии имеет смысл ввести еще одну операцию — размыкание. Но определим ее в общем случае, т.е. для симпатии. В результате размыкания мы получаем симпатию на том же множестве (т.е. родственную), но с меньшим числом связей. Попросту говоря, области интересов некоторых элементов заменяются на подмножества исходных областей интересов.

Размыкание связей на согласии производится таким образом, чтобы в результате мы опять получили согласие. Т.е. если из числа соседей элемента a_i исключается элемент a_j, то и из числа соседей элемента a_j должен быть исключен элемент a_i. Кратностью размыкания будем называть число исключенных связей. Причем, т.к. для согласия каждая связь — двойная, то кратность размыкания согласия в два раза меньше, чем кратность того же размыкания той же симпатии, рассматриваемой в обобщенном виде.

Очевидно, что однократное размыкание бесконечной линии превращает ее в два луча, однократное размыкание луча дает луч и отрезок (или изолированный элемент), однократное размыкание замкнутой линии приводит к отрезку, а та же операция, примененная к отрезку, расчленяет его на два отрезка (которые в общем случае могут оказаться и изолированными элементами).

В дальнейшем элементы согласий мы иногда будем называть точками.

Согласие S называется локально плоским в точке a_i, если усечение, построенное на окрестности этой точки, является замкнутой линией.

Точка a_j удалена от точки a_i на расстояние r, если длина кратчайшего маршрута между этими точками равна r. Аналогично поколению определим концентрический слой радиуса r вокруг точки a_i, как множество всех точек, удаленных от a_i на это расстояние. Таким образом, любое односвязное согласие можно разбить на множество концентрических слоев вокруг любой из его точек. Эти слои не пересекаются, и их объединение вместе с центральной точкой образует все множество элементов согласия.

Если усечение на любом концентрическом слое вокруг точки a_i является замкнутой линией, то такое согласие будет называться плоским вокруг точки a_i.

А теперь теорема, вернее, гипотеза, т.к. она пока не доказана и, не смотря на простоту формулировки, подход к доказательству отнюдь не очевиден:

Согласие, локально плоское во всех точках, является плоским во всех точках.

Плоское во всех точках согласие будем называть поверхностью.

Согласие S называется локально трехмерным в точке a_i, если усечение, построенное на окрестности этого элемента, является поверхностью.

Трехмерное вокруг точки a_i согласие — это такое согласие, в котором усечение на любом концентрическом слое вокруг этой точки является поверхностью.

И опять гипотеза: Локально трехмерное в каждой точке согласие является трехмерным вокруг всех точек.

По аналогии можно определить согласия с любым числом измерений.

Для примера рассмотрим однородные поверхности. Если окрестность каждого элемента состоит из трех элементов, то поверхность состоит из четырех элементов. Ее структура изображается в виде тетраэдра:

или .
Для четырех взаимностей поверхность представляет собой октаэдр:

или .
Если число связей — 5, то получаем икосаэдр:

или .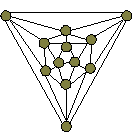
Однородная поверхность с шестью взаимностями — это бесконечная мозаика:

.
Вот фрагмент однородной поверхности с числом связей на элемент, равным 7:

.
Интересно проследить зависимость длины окружности (т.е. замкнутой линии, состоящей из точек, принадлежащих к концентрическому слою) от радиуса для однородных поверхностей с разным числом взаимностей на элемент.

Число взаимностей	Длина окружности при разных r
	r = 1	r = 2	r = 3	r = 4	r = 5	r = 6
3	3
4	4	0
5	5	5	0
6	6	12	18	24	30	36
7	7	21	56	147	385	1008
8	8	32	120	448	1672	6240

Каждая строка получается по следующему правилу: нулевое значение (т.е. при r = 0) равно 0 (в таблице не показано), первое значение равно v (числу связей на точку), каждое следующее значение вычисляется по формуле:

.
Мы видим, что зависимость длины окружности от радиуса задается последовательностью, которая является помесью геометрической прогрессии с рядом Фибоначчи. Исследование этой последовательности само по себе увлекательное занятие. Приведу только общую формулу для длины окружности (r — радиус, v — число связей точки):

.
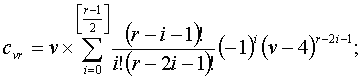Однако и без детального исследования видно, что при v < 6 отношение (аналог числа 2π) уменьшается с ростом радиуса, т.е. кривизна поверхности положительна, при v = 6 — постоянно ( = 6) и не зависит от радиуса — поверхность плоская, а при v > 6 отношение возрастает, т.е. мы имеем дело с отрицательной кривизной.

Из всего сказанного следует еще один важный вывод: «реальную» геометрическую плоскость невозможно смоделировать в виде однородной дискретной поверхности (понимаемой как согласие), т.к. единственная плоская поверхность имеет = 6, а «реальная» плоскость = 2π ≈ 6,28… . Однако, это еще не значит, что нельзя получить нужное отношение как предел при r → ∞ для какой-нибудь из неоднородных поверхностей. Такая поверхность вполне годится для «квантования» плоскости на микроуровне. То есть, если наше пространство дискретно на микроуровне, то оно, по крайней мере, неоднородно, т.е. разные точки его обладают различными свойствами. Вопрос о том, сколько разновидностей точек участвует в такой модели пространства и, в частности, плоскости, и каким образом они связаны друг с другом, остается пока открытым.

А сейчас попытаюсь доказать первую из выдвинутых гипотез, но предварительно докажу такое утверждение: если локально плоское во всех точках согласие содержит хотя бы одну точку с числом связей 3, то связная область, содержащая эту точку, состоит из четырех точек.

Пусть для точки a число взаимностей равно 3, т.е. точка a связана с тремя точками b, c и d. Т.к. согласие локально плоское в точке a, то точки b, c и d образуют замкнутую линию, т.е. существуют связи b–c, c–d и b–d. Рассмотрим точку b. Согласие локально плоское в этой точке, т.е. ее окрестность образует замкнутую линию. В эту окрестность входят точки a, c и d. Больше ни одна точка не может входить в окрестность точки b, т.к. a, c и d уже образуют замкнутую линию. Так же точно, и окрестности точек c и d не содержат других точек, кроме уже упомянутых, т.е. ни одна из точек a, b, c, d не связана с какими-либо иными точками, и a, b, c, d образуют связную область.

Отметим, что эта связная область является поверхностью (тетраэдр).

Еще одно вспомогательное утверждение. Если согласие локально плоское во всех точках, и n–й концентрический слой вокруг какой-либо точки состоит из трех точек, связанных в треугольник, то n+1–го концентрического слоя не существует.

Пусть слой состоит из трех точек b, c и d. Имеются связи b–c, c–d и b–d. Тогда окружение точки d состоит из отрезка b–c и еще нескольких точек, лежащих либо в n-1–м слое, либо в n+1–м слое, причем эти точки вместе в точками b и c образуют замкнутую линию. Но n-1–й слой обязательно содержит хотя бы одну точку из окрестности точки d. Значит, n+1–й слой таких точек не содержит. Точно так же он не содержит и точек из окрестностей b и c, т.е. не содержит вообще ни одной точки.

Саму гипотезу докажем по индукции. Окрестность любой точки в силу локальной плоскостности является замкнутой линией. Т.е. первый концентрический слой всегда является замкнутой линией. Предположим, что n–й концентрический слой вокруг какой-либо точки является замкнутой линией. Если эта линия содержит ровно 3 точки, то это последний концентрический слой, и теорема доказана. Если же число точек больше трех, то обозначим через a, b, c, d четыре последовательных точки из этой замкнутой линии. Т.е. мы предполагаем существование связей a–b, b–c и c–d.

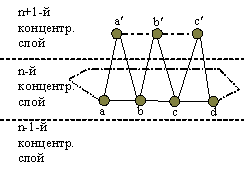
В окрестность точки b входят точки a, c и два отрезка (возможно, вырожденных в точку), один из которых лежит в n-1–м концентрическом слое, а другой — в n+1–м концентрическом слое. Пусть последний отрезок начинается точкой a' и кончается точкой b'. Для окрестности точки c соответствующий отрезок, лежащий в n+1–м слое, начинается с точки b' и кончается точкой c'. Т.к. конечная точка первого отрезка является начальной точкой второго, то a'…c' также образуют отрезок. Т.к. точки n–го слоя образуют замкнутую линию, то и последовательная стыковка отрезков в n+1–м слое также даст замкнутую линию.

Таким образом, наглядно, хотя и не совсем строго мы доказали, что локально плоское во всех точках согласие является плоским вокруг всех точек.

Еще несколько замечаний о вырожденных случаях для линии (эти замечания более уместны были бы раньше, когда мы рассматривали линии, тем более, что кое-что из того, что сейчас будет сформулировано, мы уже неявно использовали в доказательствах, но — лучше поздно, чем никогда). Отрезок мы определили, как связное согласие линейного типа, содержащее два концевых элемента. Таким образом, отрезок минимальной длины содержит две точки, обе являются концевыми, а длина отрезка равна 1. Вырожденным случаем отрезка будем считать изолированный элемент, не смотря на то, что он содержит всего 1 элемент без связей (а не 2 элемента с 1 связью каждый). Длина вырожденного отрезка равна 0.

Замкнутая линия по определению может содержать не менее 3 элементов. Введем вырожденный случай замкнутой линии из одного изолированного элемента. Возможен также другой случай вырождения замкнутой линии — это элементарный отрезок из 2 концевых элементов (этот случай не использовался в наших доказательствах).

Минимальная поверхность состоит из 4-х элементов (тетраэдр). Вырожденная поверхность также представляет собой изолированный элемент. Интерпретация изолированного элемента как частного случая поверхности может быть полезна при рассмотрении трехмерных согласий и, в частности, при доказательстве теоремы об эквивалентности локальной и глобальной трехмерности. Возможны также «частичные» вырождения поверхности до замкнутой линии из 3 элементов и до отрезка из 2 элементов.

Ну и, наконец, о минимальных и вырожденных случаях трехмерных согласий можно сказать почти то же самое:

• Минимальное 3-мерное согласие — 5 элементов (объемноцентрированный тетраэдр)

• Вырожденное 3-мерное согласие — 1 элемент (изолированный)

• Частичные вырождения — до минимальных поверхности, замкнутой линии, отрезка.